Motion in a straight line ===>Notes

Definitions

Two branches in physics examine the motion of objects:

1. Kinematics: describes the motion of objects, without looking at the cause of the motion (this is what we will be focusing on now)
2. Dynamics: relates the motion of objects to the forces which cause them (dynamics pops up later on in Physics 20).

"Quantity" is the root word for "quantitative" measurements. This means you're supposed to get a number answer. Aqualitative measurement describes qualities of the data.

In kinematics and dynamics we will discuss two kinds of measurements (quantities):

1. scalar: scalars have magnitude (a number value), but no direction
   e.g. time, mass, distance. Mass is a great example, since it has a number value (like 58 kg), but we don't give it a direction (like "down").
2. vector: have magnitude and direction
   e.g. velocity, force, displacement. Force has a number value (like 37 N) and a direction (like "pushed to the left").

Position & Time

In kinematics we need to be able to have a way to describe the motion of the objects we will be studying, whether it's a car or an atom.

The most basic information you must have to describe the motion of an object is itsposition and the time it was at that position.

• The position of an object is always taken from some reference point (which is usually "zero" on the scale).
  • Although we use the words "distance" and "displacement" interchangeably in everyday language, they mean very different things in physics.
  • The distance between two objects is scalar, since it doesn't matter which direction you measure it from. e.g. "We are standing 2.3m apart."
  • The displacement of an object is a vector, since you have to state the direction the object has traveled. e.g. "The car moved 2.56km east."

The most simple formula for calculating the change in an object's position is…

Δd = d_f - d_i

• The Δ symbol is the greek letter "delta" and means "a change in…"
• The subscript "f" and "i" stand for final and initial.
• So, in this formula, we calculate the change in position of an object by taking the final position minus the initial position.

Notice that the word "determine" has been bolded in the question. This is a "directing word" telling you what to do in the question. Get used to seeing these, since they are used on the Physics 30 diploma.

Example 1: A truck is passing a mark on the road that says 300m, and then passes another one 10s later that says 450m. Determine the distance the truck moved.

Δd = d_f - d_i = 450 - 300 = 150m

Note: If the example had asked for the displacement, we would have to include a direction (like "east") in our answer.

Average Velocity

This leads to the first major formula for the calculation of "average velocity".

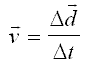
v = velocity (m/s)
Δd = displacement (m)
Δt = time (s)

• It is called "average velocity" because it does not take into consideration all the slowing down or speeding up during the object's movement.
• Instead, all you consider is the total displacement divided by the total time.
• When you write the formula, you can skip putting in the delta symbols, and the arrows (they're just there to remind you that those are vectors).

Example 2: I try to run the 100m race to break the world's record! Unfortunately, it takes me 16.83s to complete the run. Determine my average velocity.

v = d / t

= 100m / 16.83s

v = 5.94m/s

• This is my average velocity. It does not take into account that I have to speed up at the start of the race, or maybe slow down near the end.
• Most of the time we talk about velocity in kilometres per hour (km/h).
  • To convert m/s to km/h multiply by 3.6 (which is an exact value and has an infinite number of sig digs.)
  • The answer from above is 21.4km/h.
  • If you ever do a calculation like this, use the original number on your calculator, not the rounded off answer that you first wrote down.

Note that in the above example, the displacement and the velocity were positive numbers.

• Positive and negative tell you which direction you are going with respect to the reference point. (Remember, these are vectors.)
• A positive velocity means you are moving forward , to the right, or up, whilenegative means you are going backwards, to the left, or down.
• This is why it is so important not to confuse d_f and d_i

Example 3: A high speed train might be built between Edmonton and Calgary. It could travel between the two cities at an average velocity of +227km/h. The trip would take 1.2h. Determine how far apart Edmonton and Calgary are.

• Since I have a velocity and time that will cancel out nicely, I'll get an answer in kilometres.
• If you're uncertain, you should always change everything into standard units.

v = d / t

d = vt

= (227km/h) (1.2h)

= 272.4km = 2.7e2 km

Uniform Motion

If the velocity of an object is the same throughout the entire time, it has a constant(AKA uniform) velocity.

• You still use the same formula as for average velocity.
• Uniform motion is the easiest kind of motion to describe and measure, since it is always the same.
• In the examples you've done so far, and in most questions you'll do for now, you assume that it is uniform motion.

Instantaneous Velocity

But what about when you are calculating the velocity of an object traveling without uniform velocity?

• This is what would be the situation if you ask your friend how fast she is driving when you're in a car.
• She'll glance down at the speedometer and tell you how fast she is going, but that is only how fast she was going at that instant of time!
• A split second later, she might be going a bit faster or a bit slower. Most people don't drive their cars at a totally constant velocity.
• That's why we call the measurement she gave you an instantaneous velocity.

Velocity vs Speed

One last note for you. Avoid using the word "speed" when describing any velocity.

• Speed is a scalar quantity (it doesn't have direction).
• We usually want the velocity of an object.

"What speed did you drive today along Yellowhead?" -> "I drove at 72km/h."

"What was your velocity along Yellowhead?" -> "My velocity was 72km/h East."